新闻活动

1、摘要

本文提出一种评估激光定向能量沉积(L-DED)中残余应力影响的新方法。该方法重点利用快速发展的工具（如机器学习和多项式混沌展开）来处理用于测量和预测的全场数据。具体而言，通过测量薄壁L-DED钢试样的热膨胀系数，进而预测增量钻孔试验中钻孔周围的位移场。增量钻孔测试在立方体L-DED钢试样上进行，并使用3D显微数字图像图像相关（3D-Micro-DIC）装置实现位移场的可视化。预测结果与实验测量数据呈现良好吻合。

2、引言

近年来，激光技术在增材制造等众多领域中的应用日益显著。激光定向能量沉积(L-DED)作为一种增材制造工艺，通过同步输送能量与材料（通常为粉末）来逐层熔覆与凝固，从而制造出实体零件。该工艺虽能生产出所需模具极少且二次加工相对较少的零件，但层叠打印过程中产生的热应变会不可避免地引入残余热应力。这些残余应力与变形共同构成逐层打印工艺中热应变的固有属性，并导致制造零件的力学性能发生改变，特别是降低其断裂抗力和疲劳寿命，因此对其进行准确量化至关重要。

然而，由于L-DED制造零件表面存在粗糙度及由激光局部加热导致的缺陷，传统局部测量方法（如应变片）难以准确表征残余应力的影响。全场测量技术（如数字图像相关）为此提供了解决方案，它能获取试样表面全面的位移场数据。但即使获得了全场数据，其处理和有效利用仍面临挑战。

因此，本研究提出一种量化L-DEDAISI316L不锈钢零件残余应力影响的新方法。该方法聚焦于利用DIC图像获取的全场数据，以同步提升测量与预测的精度。为此，本研究将机器学习(ML)与混沌多项式展开(PCE)等潜力快速增长的工具与数值有限元模型相结合。在测量与预测环节均采用基于ML和PCE的元模型，构建实验与有限元模型间的桥梁，从而充分释放全场数据的潜力。

3、目标与结构

本方法旨在利用ML和PCE这两种最受推崇的数据处理技术，将实验全场数据与数值FE模型进行集成。该方法分为两部分，一部分与测量相关，另一部分与预测相关。尽管两部分都涉及残余应力效应的量化，但它们存在固有的差异，可总结如下：

与测量相关的部分侧重于提取薄壁L-DED AISI 316L不锈钢试样的材料属性。在此过程中，采用ML与PCE技术，将全场DIC位移场的点状数据与数值有限元模型进行匹配。此方法确保模型在局部与全局层面均能模拟试件行为，从而实现材料特性的提取。所考虑的材料属性是稳态热-力耦合模拟的必需参数，例如热膨胀系数。

与预测相关的部分则侧重于将测得的热膨胀系数纳入IHD试验的随机热-力耦合有限元模型。该IHD试验采用残余应变分析仪(ReSA)实验装置进行，该装置首次应用于L-DED AISI316L不锈钢部件。ReSA实验装置通过3D-Micro-DIC系统实现原位测量，其全场数据用于与基于随机PCE的元模型结果进行对比。该方法可高精度预测钻孔周围的位移场分布。

4、材料与方法

本节介绍前述两种测试方法所用的试样及测试过程。

4.1.热膨胀系数

试样制备：采用激光定向能量沉积（L-DED）工艺，在MiCLAD设备上使用PowderRange 316L不锈钢粉末制造。试样为薄壁结构，该试样先采用100层（预设壁,Pre-wall）打印而成，然后进行去应力退火处理（675℃温度持续2h50min，再自然冷却至室温）,以消除初始残余应力；随后在顶面追加打印20层（后处理壁,Post-wall）。

测试原理：利用后壁沉积时产生的热量传导至已冷却的预壁，引起预壁温度升高并发生热变形。通过分析因施加热量而导致的试样变形来确定热膨胀系数。

试验设置：使用数字图像相关（DIC）技术测量变形，

 · 光源：OSRAM Blue-X-Focus LED；

 · 相机：两台PointGrey相机，配Edmund Optics 35 mm f/1.65镜头；

 · 软件：VIC-3D 9，子区135像素，步长7像素；

 · 像素尺寸约15 μm，满足测量精度要求；

系统测量了两个阶段之间的位移：①初始阶段为预设壁退火冷却至室温时的位移；②最终阶段为试样在添加20层后处理壁发生变形时的位移。在DIC测量中，初始阶段与最终阶段均选取相同的感兴趣区域(ROI)。

关键设计考量：选用薄壁试样是为了增强热变形响应，并减少体积效应误差。

图1. 薄壁试样的DIC图像。(a) 预设壁几何形状，边界用蓝色标示；(b) 添加20层后的后处理壁几何形状，边界用黄色标示；(c) 参考状态下DIC使用的ROI；(d) 因膨胀导致的后处理壁几何形状表面变形W(Y,Z)，其中W为Z方向的面内变形。这些值仅为示意性，并未在分析中明确使用。

4.2.增量钻孔法

使用与前述测试相同的材料和工艺制备三个立方体试样，经铣削和顶面抛光后，最终尺寸为：24.9mm×12.2mm×20.4mm（长×宽×高）。

试验设置（增量钻孔法，IHD）：

使用ReSA残余应力分析系统，集成3D-micro-DIC系统。

DIC配置：

 · 视场（FOV）：8.4 mm × 7.0 mm；

 · 相机：Sony IMX250 2/3”CMOS单色传感器（2448×2048 Px@75FPS）；

 · 光源：Blue-X-Focus LED光源（200 W@100Hz, 1 µs闪光周期）；

 · 图像处理：VIC-3D软件，子区39像素，步长5像素，辅以拉格朗日滤波器进行图像平滑。

钻孔参数：钻孔以0.2 mm的步长进行，使用无刷风冷高速钻，扭矩可控，最高转速达50 k rpm，钻孔直径为3.2 mm。

图2. 用于IHD测量的ReSA残余应力分析系统实验装置

在每个钻孔步长采集20张图像，取平均值以降低噪声；位移场通过将当前状态图像与初始未钻孔参考图像进行对比获得。

关键设计考量：采用高分辨率3D-micro-DIC结合多次图像平均，有效应对IHD测试中位移量级极小（微米级）和表面噪声挑战，从而获取可靠的全场位移数据。

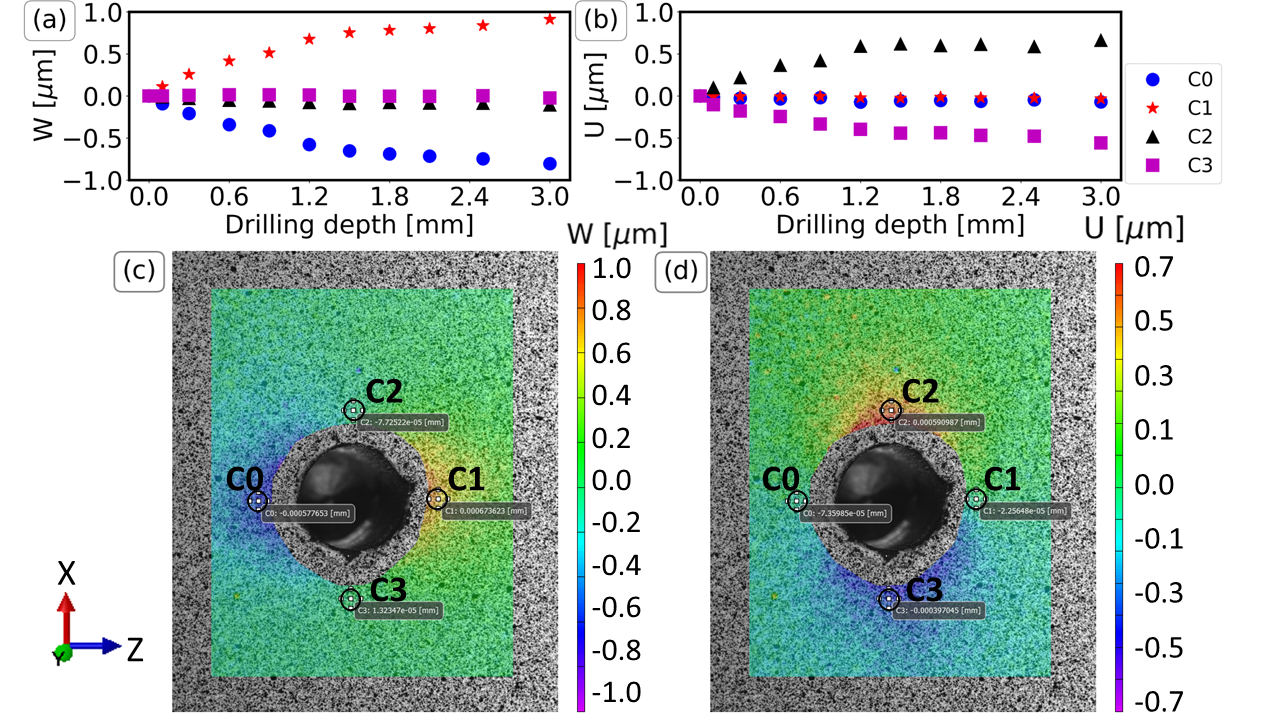
图3. 四个点C0、C1、C2、C3的位移W(a,c)和U(b,d)的DIC结果。图(a,b)展示了不同钻孔深度的平均值。图(c,d)（如VIC-3D中所见）展示了钻孔深度为1.2 mm时的位移场。

5、随机建模与优化

5.1.热膨胀系数评估

通过Nelder-Mead算法对热膨胀系数α进行评估，具体操作是将DIC系统测得的实际位移与FE模型估算的位移之间的差异进行最小化处理。目标函数F(a)如下：

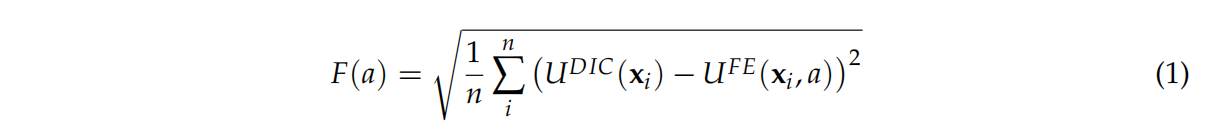
其中n为网格点总数，x为位移矢量，u为位移场，a为热膨胀系数。

不幸的是，如Nelder-Mead算法等传统优化算法需反复调用高成本的有限元模型，计算开销大，因此此处引入元模型（Metamodel）作为数值模型的替代品，以减少计算工作量。

5.1.1.元模型的开发

元模型(Uˆ FE(x, a))是一种替代有限元模型的代理模型，用于预测位移场。本文探讨并比较了两种元模型生成方法。第一种方法采用监督式机器学习，即通过线性模型拟合有限元模型在每个生成样本上评估的位移场。第二种方法则采用基于 PCE 的点配置方法。

元模型作为中间步骤引入，用于连接样品表面各点x处的位移拟合与不同热膨胀系数a值对应的行为。0级（L0或内部级）指用于表示表面位移场的元模型。L0用Û0(x)表示，它不是a的函数。1级（L1或外部级）指用于表示不同热膨胀系数值下表面位移场Û0(x)的代理模型。L1用Û1(x, a)表示，它是a的函数。

 · L0级（内部级）：基于DIC实测数据，采用机器学习方法，选取三阶多项式并通过最小二乘法拟合构建表面位移场元模型Û0(x)；

 · L1级（外部级）：建立位移场对热膨胀系数a的响应关系Û1(x,a)，采用两种方法：①监督机器学习（ML）：线性回归拟合；②混沌多项式展开（PCE）：基于Sobol序列采样 + 点配置法。

决定系数R^2被用于两种方法，以评估元模型捕捉有限元模型变异性的能力。两种方法(以及L0和L1两个层次)的系数均计算在0.97至0.999之间，由此证实元模型能准确表征位移场。

5.1.2.薄壁试样数值建模

本分析核心是开发能准确代表薄壁试样的有限元模型。此处，使用ABAQUS软件进行有限元建模。FE模型的构建代表了如图4a所示的薄壁几何形状，该尺寸取自实际L-DED加工的AISI 316L不锈钢几何形状。

图4. 薄壁试样的有限元模型。(a) 基于对称性创建和分割的完整模型；(b) 打印层厚度；(c) 添加钢材（白色）和刚性基材（绿色）；(d) 网格结构；(e) 用于提取位移的节点（红色）。

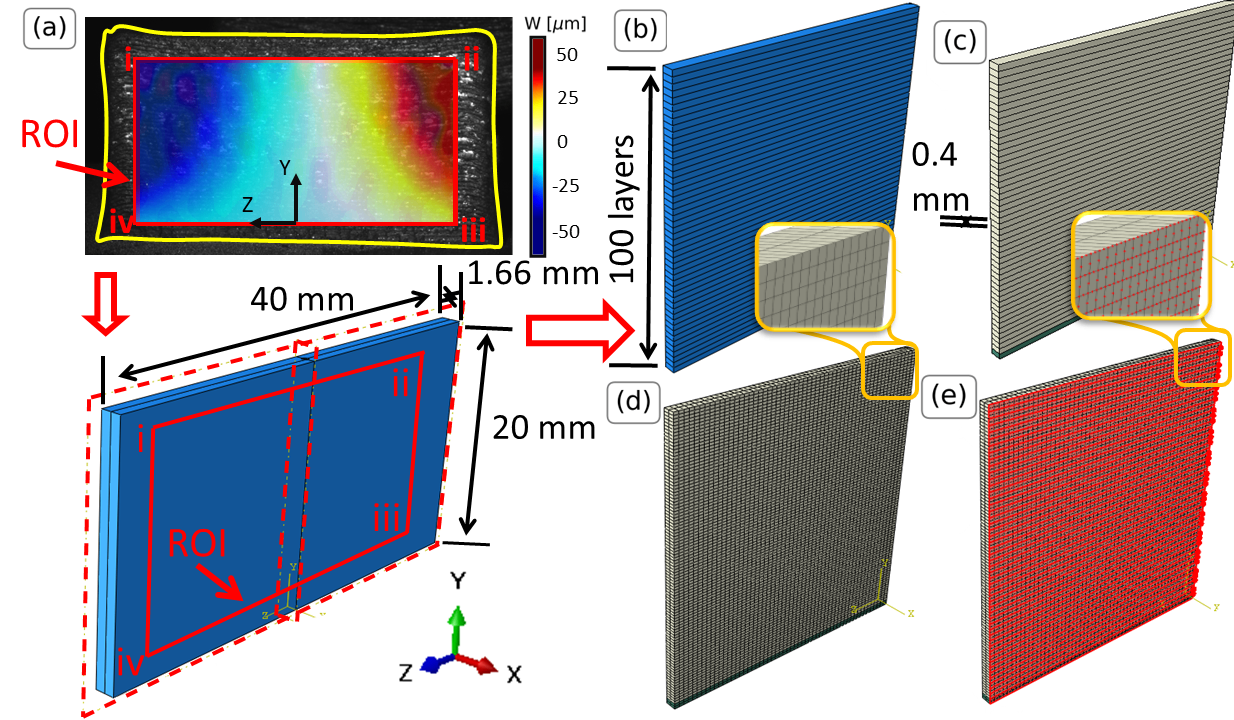
由于问题在X-Y平面和Y-Z平面具有对称性，仅考虑试样四分之一区域(图4b)，并在相应表面施加对称边界条件。Y-Z平面上的对称边界条件限制了U方向位移及绕Y轴和Z轴的旋转，而X-Y平面上的条件则限制了w方向位移及绕X轴和Y轴的旋转。几何结构沿Y轴方向分段划分，以体现沉积过程中形成的不同打印层(图4b)。本研究采用AISI316L不锈钢材料，其杨氏模量为138GPa，泊松比为0.29。

热膨胀系数作为一个随机变量，从均匀分布中选取，下限为常规钢的值（10.5 × 10⁻⁶/°C），上限为L-DED加工的AISI 316L不锈钢对应的值（17.62 × 10⁻⁶/°C）。底层(绿色)采用相同弹性特性但极低热膨胀系数构建，形成对温度变化具有"刚性"的材料。此设计旨在描述材料因与打印平台相互作用及平台热扩散而无法移动的特性。两种材料在图4c中可视化呈现。

温度场在Y=0处的印刷板与第100层之间按线性关系设定，印刷板视为处于环境温度(298K)，第100层温度介于700至1100K之间，本文将其视为随机变量(类似于热膨胀系数)，遵循均匀分布。基于网格收敛性研究，最终采用11,600个三维二次缩减积分20节点单元(C3D20R)。网格化几何结构如图4d所示。后处理阶段通过定制Python脚本导出前表面节点位移(图4e)。

4.1.3. 结果

基于上述内容，通过最小化目标函数实现热膨胀系数的估算：

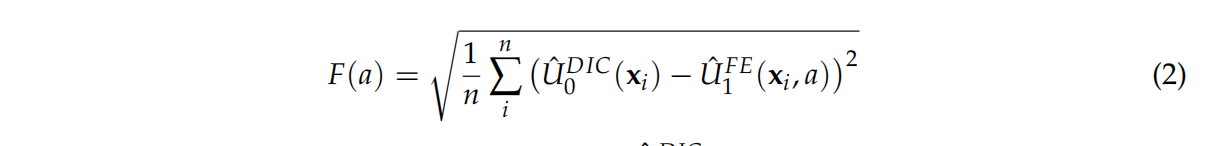
其中n为网格点总数，ÛDIC₀(x)是根据DIC数据拟合的L0元模型，可用于评估ÛFE₁(x, α)确切位置上的位移场。

表1汇总了两种元模型方法(ML和PC)在Z方向(a)和Y方向(a)的热膨胀系数值。采用方差分析(ANOVA)检验四组测量值的均值是否存在显著差异。结果表明，在95%置信水平下(p值=0.20)四组数值间无显著差异。因此研究发现，ML与PC的L1元模型在两个方向上测得的热膨胀系数均具有相近精度。这些数值将纳入IHD测试的随机建模过程。

表1.通过最小化L1元模型(ML和PC)估算的热膨胀系数，分别沿Z方向(a-)和Y方向(ay)。

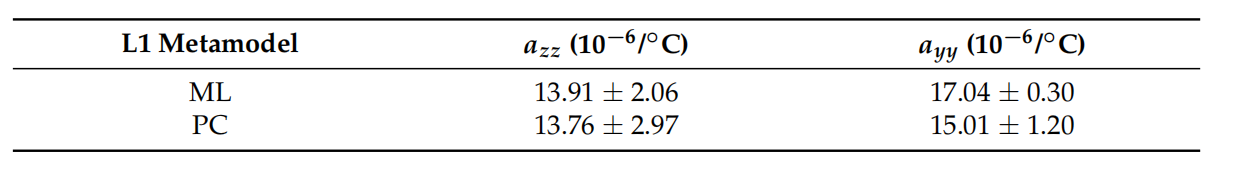
5.2. 增量钻孔法位移场的随机建模

本节描述了对L-DED加工的AISI 316L不锈钢零件IHD测试位移场的随机建模。

5.2.1. 增量钻孔法的数值建模

增量钻孔(1HD)试验分阶段进行。在钻孔前固定动态图像分析(DIC)装置并拍摄顶面初始参考图像。随后按钻孔深度的固定间隔分阶段实施钻孔。每次间隔期间均采集顶面图像，并与初始参考图像对比以提取位移场。

位移场是由打印过程中在试样中产生的残余应力所形成的。冷却后，试样处于"预应力"状态。该预应力状态必须作为IHD前的基准状态。由于残余应力值未知，无法在模型中精确施加于每个单元。但可通过模拟试样制造、打印及冷却过程的模型进行近似处理。

鉴于上述情况，并考虑到残余应力的成因是试样冷却，可通过施加负的稳态温度场来替代制造过程的建模。 负温度场模拟冷却过程，最终使试样处于预应力状态，其体积内存在残余应力。该状态可作为测量位移场的基准。本文采用有限元法对该过程进行模拟。

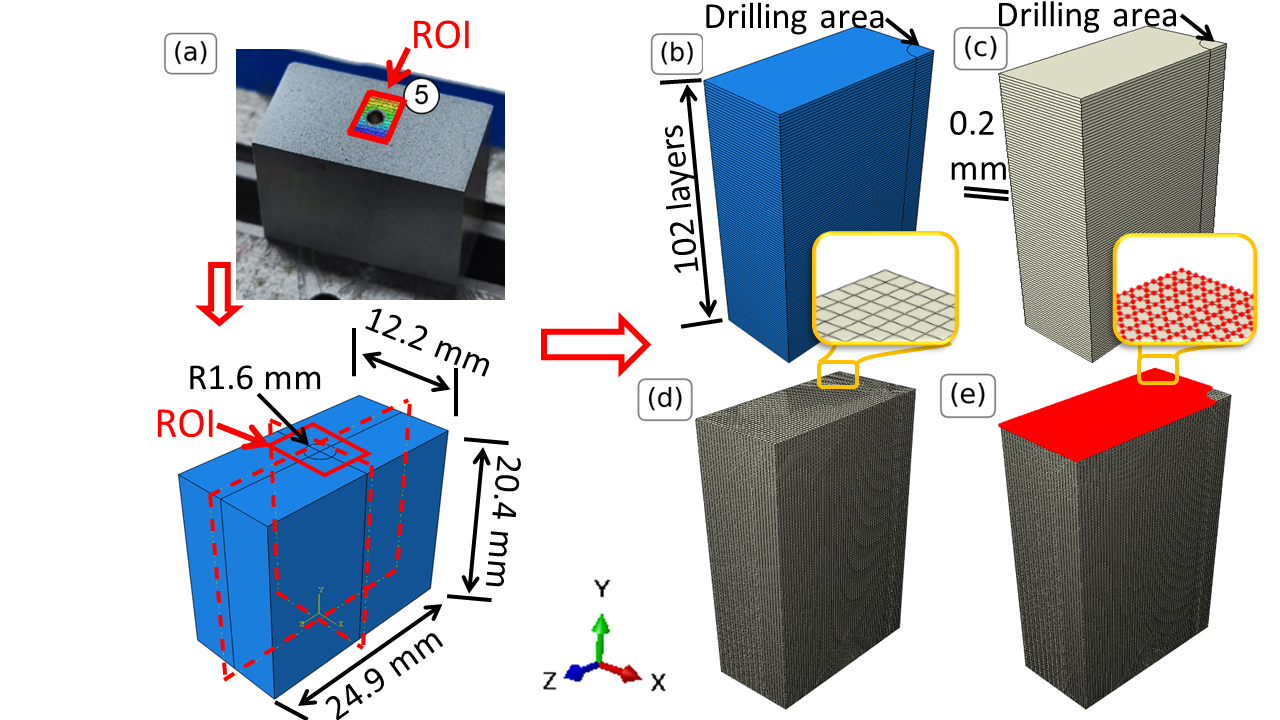
图5.IHD测试的有限元模型。(a)基于对称性创建并划分完整模型，(b)打印层厚度，(c)建模所用钢材(白色)，(d)网格化结构，(e)提取位移的节点(红色)。

用于描述IHD测试的有限元模型与前述评估热膨胀系数所用的模型相似。其几何结构如图5a所示。为体现问题的对称性，结构沿X-Y平面和Y-Z平面进行划分(图5b)。此外，结构还沿钻孔方向Y轴进行分段划分，以体现不同的钻孔深度。

在坐标系原点处划分一个贯穿试样所有层的圆柱体。该划分将用于建模IHD测试，其应用将在下文阐述。所有层均施加线性温度场，底层温度为298K，顶层为最高温度。最高温度值在1050-1450K范围内视为均匀分布。为模拟收缩并诱导残余应力，将温度差以负值形式叠加。材料属性与第5.1.2部分一致，热膨胀系数取自表1结果。根据网格收敛性研究，模拟共使用近82000个C3D20R单元。图5d展示了网格化状态下的模型。

图6.显示不同钻孔深度下IHD测试模型的Y-Z平面视图，其中钢材部分(白色)与空隙区域(红色)清晰呈现。(a)钻孔深度0.0mm，(b)钻孔深度0.4mm，(c)钻孔深度2.0mm。

到目前为止，已经对一个带有残余应力（预应力几何形状）的立方体试样进行了建模，下一步是在此几何形状上（虚拟地）执行IHD测试。IHD通过不同钻孔深度的连续模拟进行建模。所有圆柱形分区直至钻孔深度均采用弹性模量极低的材料建模，从而模拟出钻孔空腔段。图6展示了不同钻孔深度的几何结构示例。红色区域表示试样中被钻孔的部分，该区域的单元具有极低的刚度。通过在连续模拟中增加钻孔深度，可实现IHD试验的模拟。

最后，通过Python脚本导出所有未包含在圆柱截面(图5e)中的顶面节点位移。随后，通过比较钻孔深度为0.0mm的基准模拟与后续钻孔步骤的差异，获得位移场。该过程与用于评估位移场的DIC测量方法完全一致。 由于热膨胀系数和最高温度具有随机性，主成分分析法采用第5.1.1节所述方法实现。

5.2.2. 位移场结果

现将DIC测量所得IHD试验中X轴方向位移场(U位移)与Z轴方向位移场(W位移)的结果，分别与图7-10中各元模型的预期值及标准差进行对比。因问题具有对称性，仅考虑单一象限数据。所有钻孔深度的结果均呈现相似趋势，此处仅展示1.2mm和2.0mm的钻探深度结果。需说明的是，预期值与标准差分别通过元模型的第一矩和第二矩的平方根进行估算。

总体而言，PC法很好地捕捉了DIC可视化的位移场特征，无论是在最小值与最大值的位置分布，还是钻孔周围的整体行为模式上均表现一致。在所有钻孔深度下，U方向位移在Z=0处沿X轴方向达到峰值后迅速衰减;同样地，W方向位移在X=0处沿Z轴方向达到峰值。此外可观察到，结果在X=Z处近乎对称，且最大位移随钻孔深度增加而增大。最后，PC法与DIC测量值的对比表明:试件预期W向位移(图7和9b)处于PC法预期值(图7和9f)与预期值加一个标准差区间内。试件的预期U位移(图8和10b)与PC法的预期值(图7和9e)吻合良好。

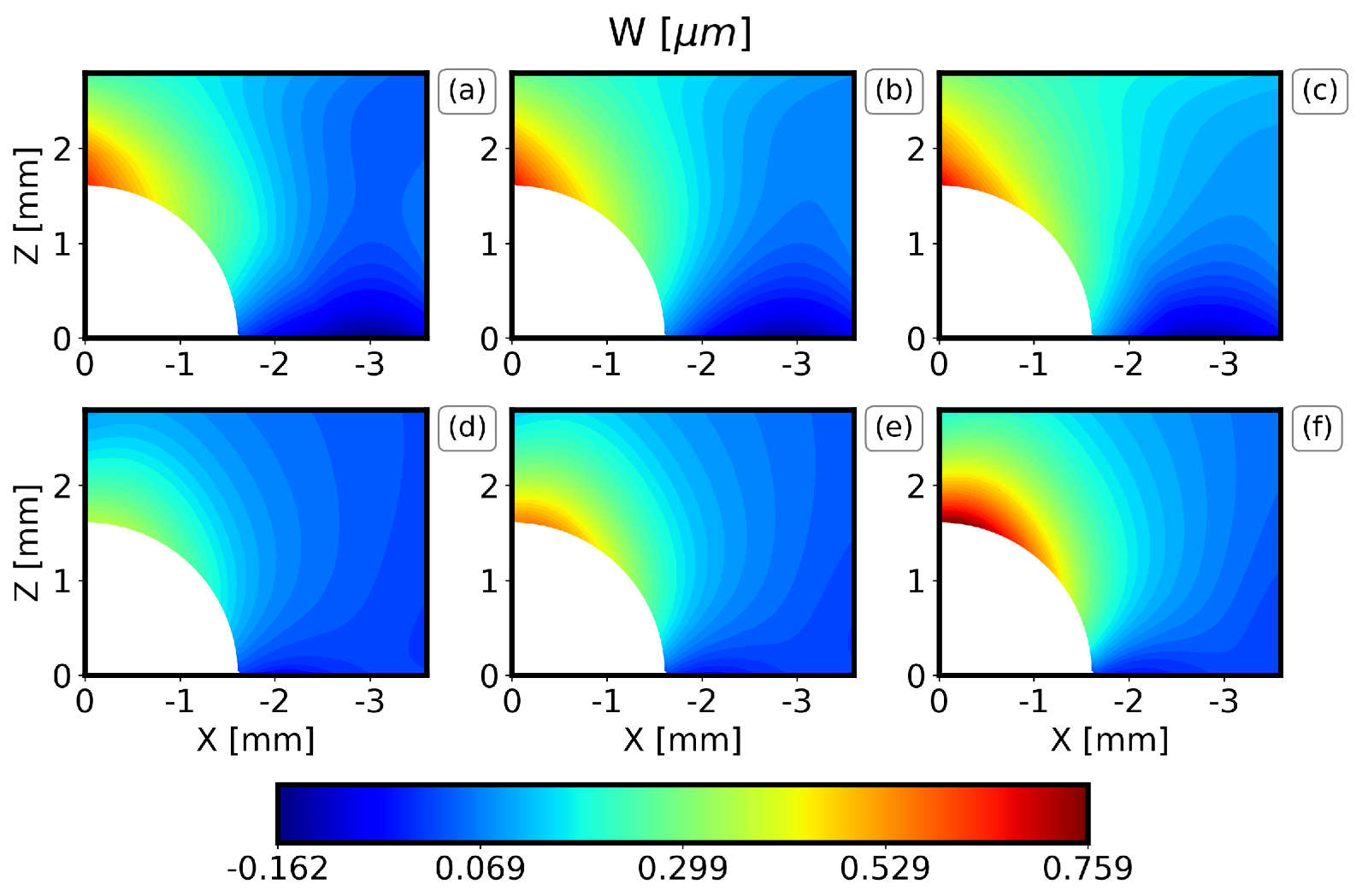
图7.位移场W在钻孔深度1.2mm时的DIC测量值与PC结果对比。(a)预期实验值减去一个标准差，(b)预期实验值，(c)预期实验值加上一个标准差，(d)预期PC值减去一个标准差，(e)预期PC值，(f)预期PC值加上一个标准差。

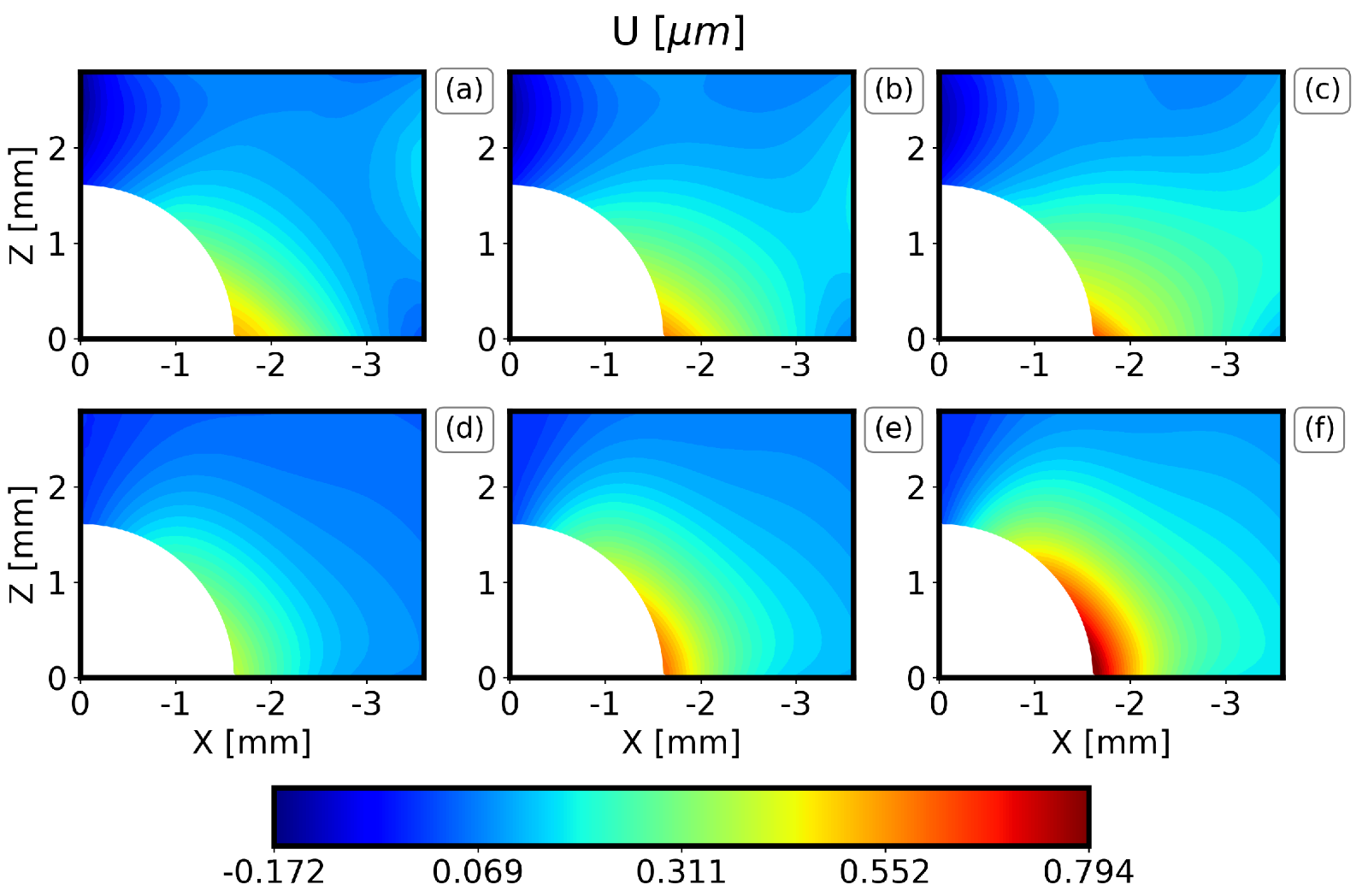
图8.位移场U在钻孔深度1.2mm时的DIC测量值与PC结果对比。 (a)预期实验值减去一个标准差， (b)预期实验值，(c)预期实验值加上一个标准差，(d)预期PC值减去一个标准差，(e)预期PC值，(f)预期PC值加上一个标准差。

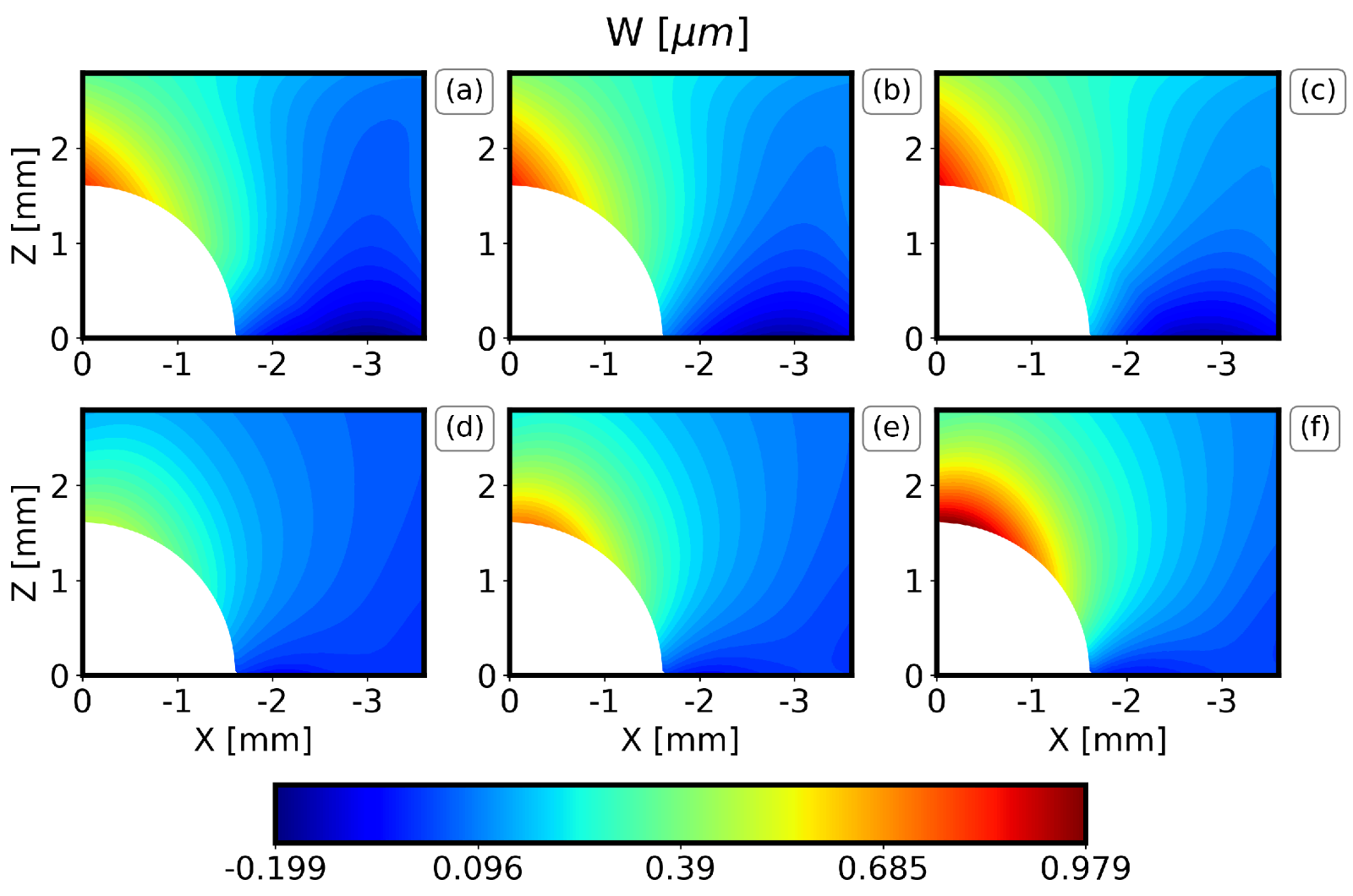
图9.位移场W在钻孔深度2.0mm时的DIC测量值与PC结果对比。(a)预期实验值减去一个标a准差，(b)预期实验值，(c)预期实验值加上一个标准差，(d)预期PC值减去一个标准差，(e)预期PC值，(f)预期PC值加上一个标准差。

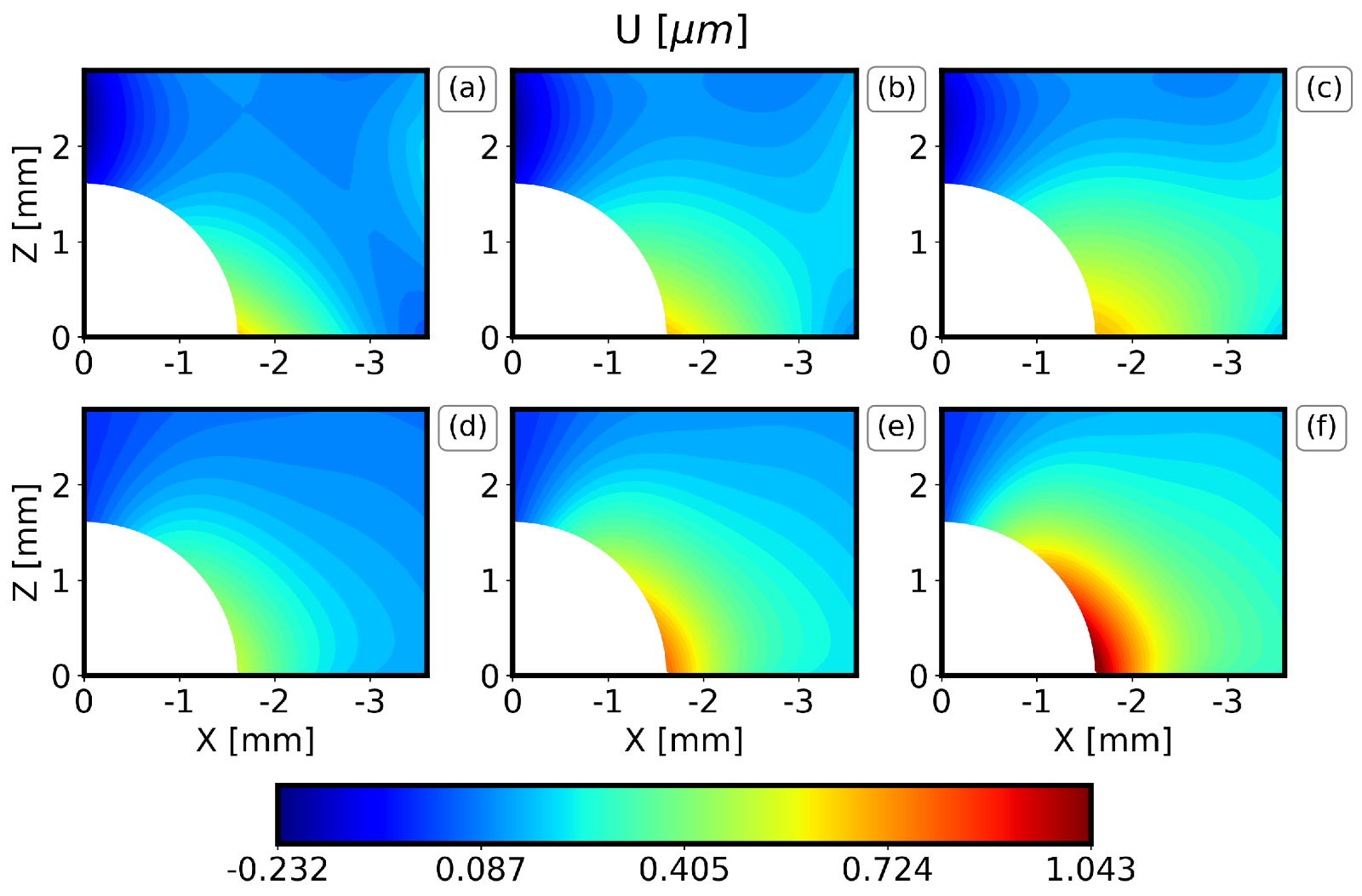
图10.位移场U在钻孔深度2.0mm时的DIC测量值与PC结果对比。(a)预期实验值减去一个标a准差，(b)预期实验值，(c)预期实验值加上一个标准差，(d)预期PC值减去一个标准差，(e)预期PC值，(f)预期PC值加上一个标准差。

6、结论

本研究致力于开发一种通过机器学习（ML）和混沌多项式展开（PCE）基元元模型，将数字图像相关（DIC）图像的全场实验数据与数值有限元（FE）模型集成，从而定量评估残余热应力影响的方法。该方法应用于激光加工的AISI 316L不锈钢零件，既可用于测量薄壁试件的热膨胀系数，也可用于预测钻孔热膨胀试验中钻孔周围的位移场。

热膨胀系数测量通过优化方案实现，该方案旨在最小化全场DIC数据与基于机器学习及PCE的元模型结果之间的误差。两种方法（ML与PCE）的对比表明，二者在估算热膨胀系数方面具有同等精度。此外，本方法获得的结果与公开文献中先前报道的结果接近。

采用PCE方法预测了IHD试验中钻孔周围的位移场。实验结果与随机模型的对比表明，钻孔周围位移场可被预测且精度可接受。

综上所述，建议采用基于ML和PCE的元模型充分利用全场DIC数据，实现实验结果与数值有限元模型的融合。

更多信息 More Information

VIC-3D 非接触全场应变/应力测量系统；3D-Micro-DIC ；ReSA残余应力测量系统；

Email: Info@acqtec.com or visit our Contact Us page to obtain a quotation.